Exciton-polariton condensates and new quantum technologies

Exciton-polariton condensates and new quantum technologies

1. Exciton-polariton Bose-Einstein condensates

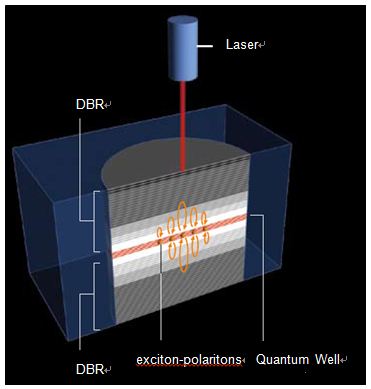
Exciton-polaritons are quasi-bosonic particles that are excited in semiconductor quantum well microcavities.  In 2006 a Bose-Einstein condensate (BEC) of these particles was created [1]. The attraction of the exciton-polariton system is that many of the same experiments that can be performed in atomic physics can be done in the semiconductor system. From a quantum information technology perspective, the semiconductor BEC system has several practical advantages over the atomic systems.  The temperatures that are usually used to form exciton-polariton BECs are in the vicinity of T=10K, far higher than the nanokelvin temperatures required for atomic BECs. By using different semiconductors it should be possible to increase these temperatures to room temperatures, opening the possibility for new devices that use the BEC effect.  BECs are promising in terms of new quantum technologies since quantum effects can appear on a macroscopic level, unlike most systems where quantum effects are rather easily destroyed by temperature and decoherence.

Figure 1: Schematic device diagram for exciton-polaritons in a semiconductor microcavity.

2. Quantum simulation

Quantum computers promise to offer a new paradigm in computation, with potentially a dramatic increase in speed in obtaining the solution of certain computational problems. One of the first demonstrations of this was Shor’s algorithm, where it was shown that the factorization of a large number into prime numbers could be performed exponentially faster on a quantum computer, compared to a classical computer.  While this was an important breakthrough, we are currently faced with two very fundamental difficulties that must be overcome before quantum computers can be used as practical devices. The first is that from a hardware perspective, quantum computers are extremely difficult to make due to problems such as decoherence.  A second problem is a software problem, in that quantum computers do not always have the dramatic speedup that Shor’s algorithm demonstrates.

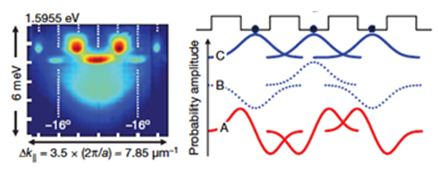
For these reasons, recently there has been a growing interest in the field of quantum simulations. The purpose of the field of quantum simulations is to build technologies that are able to simulate complex many-body problems, specifically quantum many-body problems [1].  The approach of quantum simulations is to build purpose-built devices that can simulate the quantum many-body problem of interest [2].  The attraction of quantum simulators are that they are technologically easier to realize, due to less demand on the controllability of the qubits, and thus are closer to realization than a full quantum computer. There are several approaches to quantum simulation from a technological point of view.  The first and most successful to date is using cold atoms trapped in optical lattices and ion traps [2].  The past research that I have been involved has focused on using semiconductor quantum well systems to realize quantum simulators for the Fermi-Hubbard and Bose-Hubbard models [3,4,5] (see Fig. 2).  A quantum simulator for the Fermi-Hubbard model, if realized, would be a significant breakthrough because of the strong connections it has with outstanding problems in condensed matter physics such as high-temperature superconductivity.

Figure 2:Experimental realization of a Bose-Hubbard model using exciton-polaritons (from Ref. [3]). Metallic strips on the surface of the semiconductor produce a periodic potential, creating a metastable condensate at non-zero momentum.

3. Photoluminescence characteristics

Lasers have found many practical applications in society, due to the very useful properties originating from optical coherence.  However, as is well known from the field of quantum optics, coherent light is not the only possible form of light.  The quantum properties of light can give light with many different properties: Fock states, squeezed light, Schrodinger cat states, entangled states to name a few examples. The uses of new states of light are currently being investigated in the field of quantum information technology.  Already several exciting applications such as quantum cryptography and quantum teleporation have been demonstrated using light.  However, the problem which consistently arises with quantum optical technologies is the weakness of the non-linearities that are necessary to generate these new states of light.

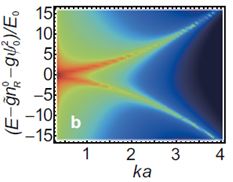
Exciton-polaritons BECs have interesting light characteristics due to the non-linear interactions that are present inside the semiconductor.  This is in contrast to conventional lasers where the photons which have no such interaction, and occurs due to the half-light, half-matter particles nature of the polaritons.  Due to their matter component, the polaritons interact with each other while they are within the cavity, and form coherence via Bose-Einstein condensation.  The light emerging from the cavity inherits the same characteristics as the polaritons, thus is expected to have different properties to standard laser light.  Our recent theoretical results have been able to handle the high density regime of exciton-polariton condensates, showing many novel features such as a Mollow’s triplet type spectrum (see research summary on the BEC-BCS crossover) and a negative Bogoliubov dispersion [6] (see Figure 3).

Figure 3: The negative dispersion of exciton-polariton condensates.

References

[1] H. Deng et al., Science 298, 199 (2002); J. Kasprzak et al. Nature 443, 409 (2006).
[2] R. Feynman, Int. J. Theo. Phys. 21, 467 (1982).
[3] I. Buluta and F. Nori, Science 326, 108 (2009).
[3] T. Byrnes, P. Recher, N. Y. Kim, S. Utsunomiya, Y. Yamamoto, Phys. Rev. Lett. 99, 016405 (2007); T. Byrnes, N.Y. Kim, K. Kusudo, Y. Yamamoto, Phys. Rev. B 78, 075320 (2008).
[4] T. Byrnes, P. Recher, Y. Yamamoto, Phys. Rev. B 81, 205312 (2010).
[5] C.W. Lai, N. Y. Kim, S. Utsunomiya, G. Roumpos, H. Deng, M. D. Fraser, T. Byrnes, P. Recher, N. Kumada, T. Fujisawa and Y. Yamamoto, Nature 450, 529 (2007).
[6] Tim Byrnes, Tomoyuki Horikiri, Natsuko Ishida, Michael Fraser, Yoshihisa Yamamoto, Phys. Rev. B   85, 075130   (2012) .